Cross Validation

What is Cross Validation (CV)

Let’s say we have 50 sets of data used to train a model. If we use all the data for training, then we don’t have any left to test it. Thus, a sensible approach is to split it 80/20, when 80% of the data is used to train the model, and remaining 20% is used to test it.

• data set 1-40: use for training
• data set 41-50: use for testing

However, we don’t know for sure if data set 1-40 is the best for training the model; neither do we used all the data available.

Cross Validation can solve the problem, or improve the model. Basically, we want to divide the data into K groups (K-folds), example 5 groups below. In each iteration / training process, 4/5 groups are used to train the model, and the last one for testing.

Dataset 1-8	Dataset 9-16	Dataset 17-24	Dataset 25-32	Dataset 33-40	Dataset 41-50
Train	Train	Train	Train	TEST	HoldOut
Train	Train	Train	TEST	Train	HoldOut
Train	Train	TEST	Train	Train	HoldOut
Train	TEST	Train	Train	Train	HoldOut
TEST	Train	Train	Train	Train	HoldOut

Hypothesis: Model trained with CV performs BETTER!

Setup

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
# create 50 data points for the experiment
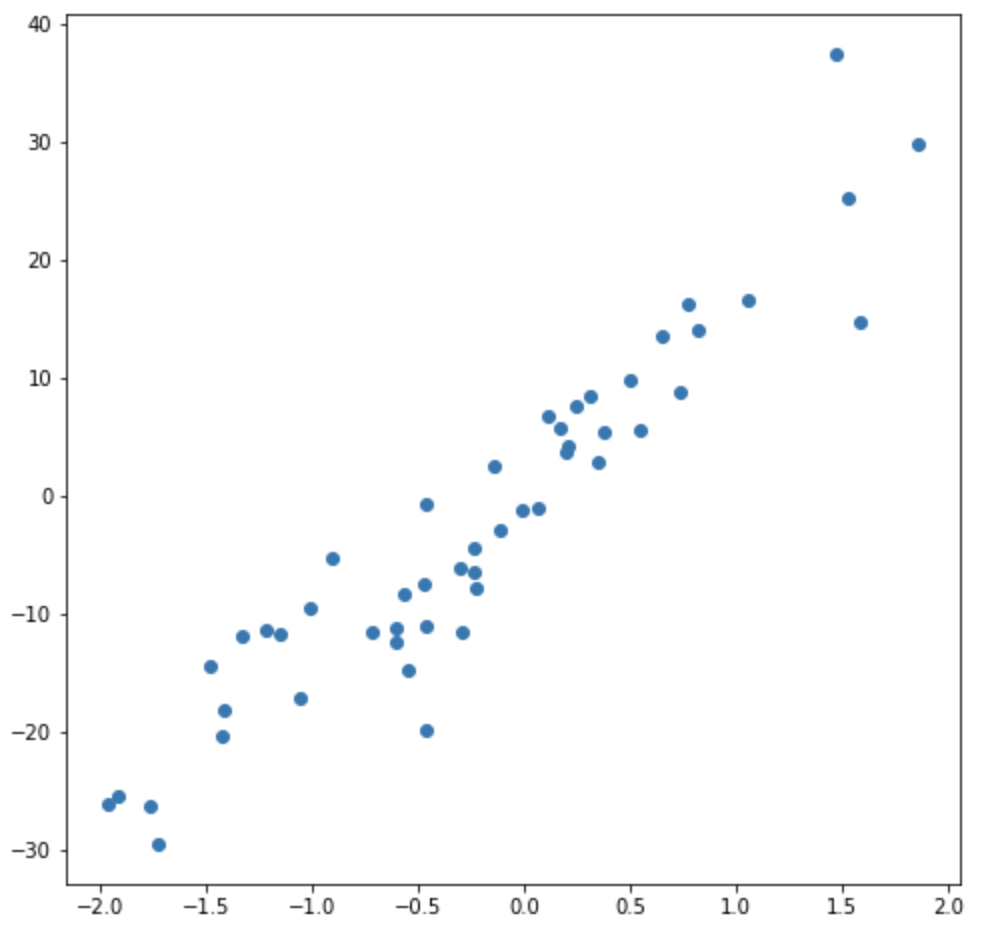
X, y= make_regression(n_samples=50, n_features=1, noise=5, random_state=42)
plt.scatter(X,y)

Split data in 80/20 with 20% for Test

from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
print("x_train: ", x_train.size)
print("x_test: ", x_test.size)

# output
x_train:  40
x_test:  10

Train model as baseline

from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
# fit linear regression model to training set
linear = LinearRegression()
linear.fit(x_train, y_train)
# predit training set and test set using the model
y_train_pred = linear.predict(x_train)
y_test_pred = linear.predict(x_test)
scores = {}
scores["training set"] = {"r_2": r2_score(y_train, y_train_pred), "mse": mean_squared_error(y_train, y_train_pred)}
scores["test set"] = {"r_2": r2_score(y_test, y_test_pred), "mse": mean_squared_error(y_test, y_test_pred)}
print(scores)

# output
{'training set': {'r_2': 0.9082211858809777, 'mse': 20.77136285727775},
 'test set': {'r_2': 0.6761171340902208, 'mse': 36.679634983592294}}

Let’s use Cross Validation

from sklearn.model_selection import cross_validate
# CV is set to 5-fold
# R^2 and mse is used as scoring metrics
scores = cross_validate(linear, X, y, cv=5, return_estimator=True, scoring=('r2', 'neg_mean_squared_error'))
print(scores)

# output
{'fit_time': array([0.00079298, 0.00041986, 0.00042582, 0.00053477, 0.00041199]),
 'score_time': array([0.00068283, 0.00073123, 0.00070882, 0.00072026, 0.00058603]),
 'estimator': (LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False),
  LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False),
  LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False),
  LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False),
  LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)),
 'test_r2': array([0.83294462, 0.87513271, 0.85425891, 0.95260985, 0.86880153]),
 'test_neg_mean_squared_error': array([-28.66454405, -15.60107755, -47.62231841,  -6.01442767,
        -34.90107707])}

We can see the 4th model performs the best, with R^2 =0.95260985, and mse=-6.01442767. Using the best model to predict:

best_model = scores["estimator"][3]
y_train_pred_cv = best_model.predict(x_train)
y_test_pred_cv = best_model.predict(x_test)
from sklearn.metrics import r2_score
scores_cv = {}
scores_cv["training set"] = {
    "r_2": r2_score(y_train, y_train_pred_cv),
    "mse": mean_squared_error(y_train, y_train_pred_cv)
}
scores_cv["test set"] = {
    "r_2": r2_score(y_test, y_test_pred_cv),
    "mse": mean_squared_error(y_test, y_test_pred_cv)}
print(scores_cv)

# output
{'training set': {'r_2': 0.9051641686456118, 'mse': 21.463226386636407},
 'test set': {'r_2': 0.725591176478181, 'mse': 31.076714894393582}}

Conclusion

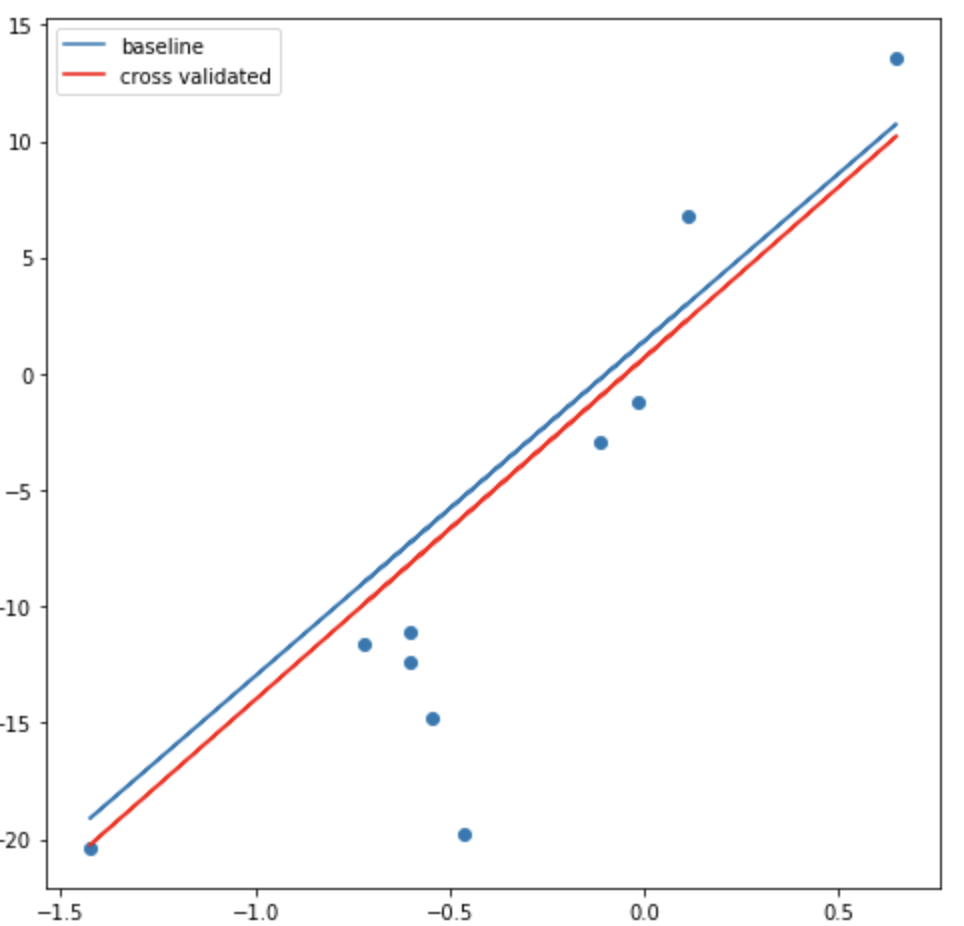
The model trained with CV performs better compared to the baseline, as

• R^2 is higher, 0.725 vs 0.676
• mse is lower, 31 vs 36

Below is the visualization below. Red line is the CV.