Logistic Regression

Logistic Regression is a classification problem whose target / output is a set of discrete values.

Binary Classification

In binary classification, the output of Y has only two values, usually 0 and 1.

• 0: the negative case, absence of the observed outcome
• 1: the positive case, the presence of the intended outcome

Logistic function of binary classification is call Sigmoid Function, its charateristic includes:

• x ranges from +∞ to -∞
• y ranges from 0 to 1
• ‘S’ shaped

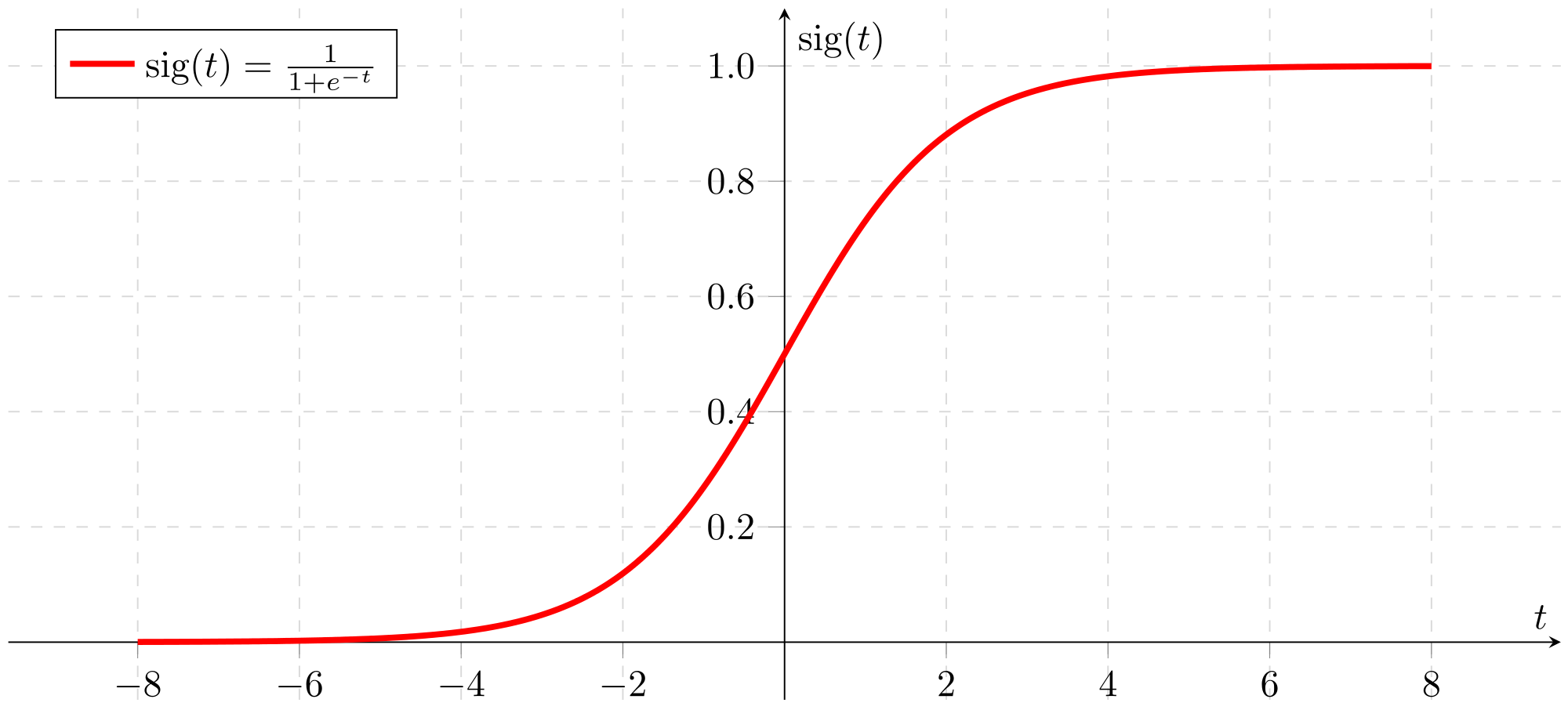
Logistic Function Equation

h_θ(x) = g(θ^Tx) = 1 / (1 - e^-θTx) when g(z) = 1 / (1 - e^-z)

h_θ(x) = P(y=1|x;θ) = 1 - P(y=0|x;θ), in other words, h_θ(x) will give us the probability that our output is 1.

P(y=1|x;θ) + P(y=0|x;θ) = 1

Translate probability to discrete values

Assume this is how we will translate the P into 0 and 1:

• y = 1 if h_θ(x) >= 0.5
• y = 0 if h_θ(x) < 0.5

Since h_θ(x) = g(θ^Tx), for h_θ(x) >= 0.5 means θ^Tx >= 0, thus:

• y = 1 if θ^Tx >= 0
• y = 0 if θ^Tx < 0

Solving the equation we get the Decision Boundary

Decision Boundary is not a property of the data set, but a property of the hypothesis and parameters.

Cost Function

The original sigmoid function is non-linear thus will not have global minimum. Log function solves the problem.

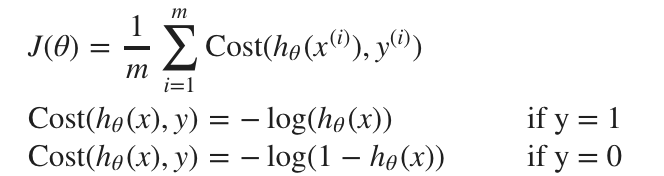
Intuition

If we correctly predict the outcome, then the cost will nearly 0

If we wrongly predict the outcome, the cost will be close to infinity

If y=1	If y=0

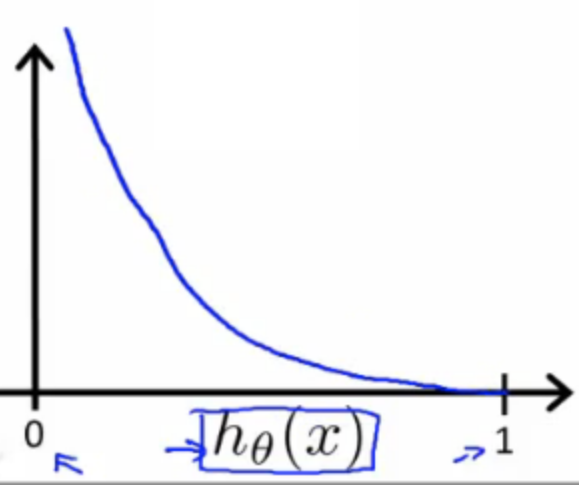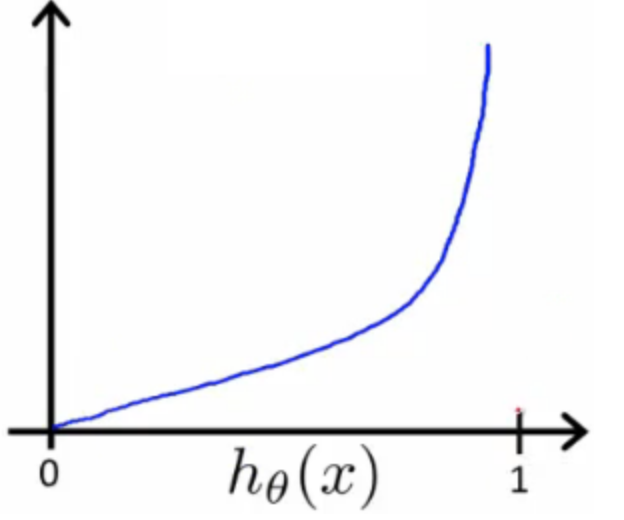Gradient Decent for Cost Function of Logistic Regression

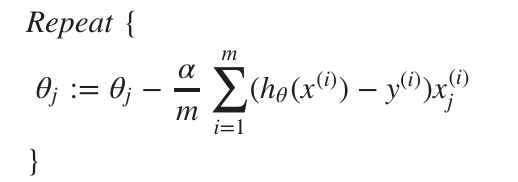
Reference: Machine Learning by Andrew